1. 문제
2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다. 이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북
www.acmicpc.net
다리 만들기
시간 제한메모리 제한제출정답맞은 사람정답 비율
| 2 초 | 192 MB | 15544 | 5247 | 3351 | 32.741% |
문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
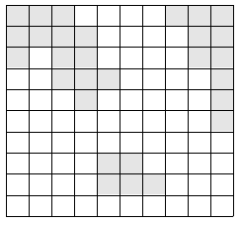
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.

물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
예제 입력 1 복사
10 1 1 1 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
예제 출력 1 복사
3
2. 소스코드
#include <iostream>
#include <queue>
#include <tuple>
#include <cstring>
using namespace std;
//0:sea 1:earth
int map[100][100];
int visited[100][100];
int n, ans = 10000;
int dx[] = { -1,1,0,0 };
int dy[] = { 0,0,-1,1 };
void bfs() {
int area = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] == 1 and visited[i][j] == 0) {
queue<pair<int, int>> q;
q.push(make_pair(i, j));
visited[i][j] = 1;
while (!q.empty())
{
auto pos = q.front(); q.pop();
visited[pos.first][pos.second] = 1;
map[pos.first][pos.second] = area;
for (int k = 0; k < 4; k++) {
int nx = pos.first + dx[k];
int ny = pos.second + dy[k];
if (ny < 0 || nx < 0 || ny >= n || nx >= n) continue;
if (map[nx][ny] == 0 or visited[nx][ny] == 1) continue;
visited[nx][ny] = 1;
q.push(make_pair(nx, ny));
}
}
area++;
}
}
}
memset(visited, 0, sizeof(visited));
return;
}
void bfs2() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] != 0) {
int areaNum = map[i][j];
queue<tuple<int, int, int>> q;
q.push(make_tuple(i, j, 1));
visited[i][j] = 1;
while (!q.empty()) {
auto pos = q.front(); q.pop();
int x = get<0>(pos);
int y = get<1>(pos);
int depth = get<2>(pos);
for (int k = 0; k < 4; k++) {
int nx = x + dx[k];
int ny = y + dy[k];
if (ny < 0 || nx < 0 || ny >= n || nx >= n) continue;
if (map[nx][ny] == areaNum || visited[nx][ny] == 1) continue;
if (map[nx][ny] != 0) {
if (ans > depth - 1) ans = depth - 1;
while (!q.empty()) q.pop();
break;
}
visited[nx][ny] = 1;
q.push(make_tuple(nx, ny, depth + 1));
}
}
memset(visited, 0, sizeof(visited));
}
}
}
return;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> map[i][j];
}
}
bfs();
bfs2();
cout << ans;
return 0;
}'알고리즘 > BOJ(백준)' 카테고리의 다른 글
| [ 백준-15686번 / 시뮬, BFS, BT ] 치킨 배달 (삼성SW) (0) | 2020.03.26 |
|---|---|
| [ 백준-16236번 / BFS ] 아기 상어 (삼성 SW) (0) | 2020.03.26 |
| [ 백준-16234번 / BFS ] 인구 이동(삼성 SW) (0) | 2020.03.20 |
| [ 백준-15684번 / ] 사다리 조작 (삼성SW) (0) | 2020.03.18 |
| [ 백준-15683번 / DFS ] 감시 (삼성SW) (0) | 2020.03.18 |

