1. 문제
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10) 입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다. 방향은 0, 1, 2,
www.acmicpc.net
문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
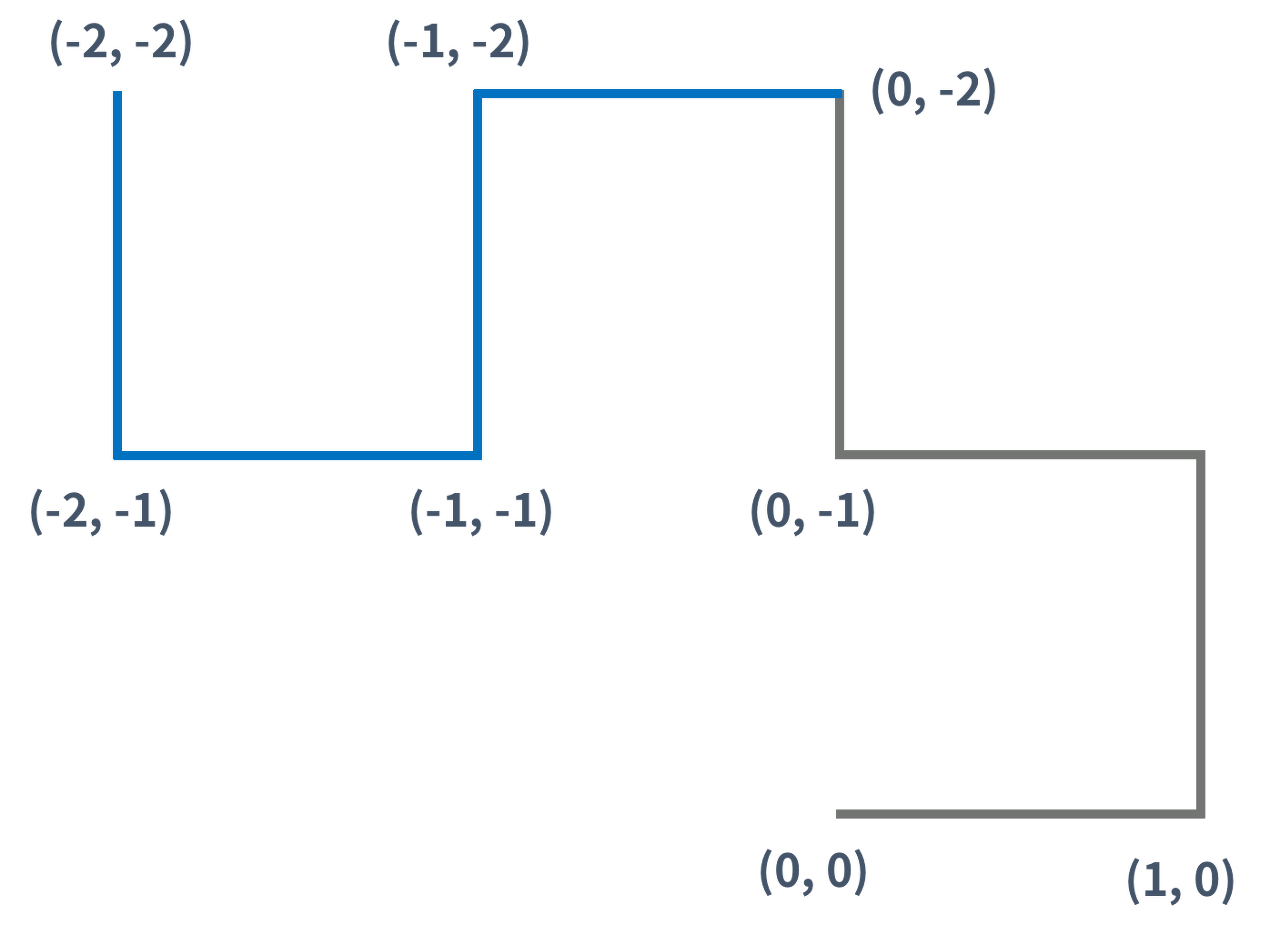
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
예제 입력 1 복사
3 3 3 0 1 4 2 1 3 4 2 2 1
예제 출력 1 복사
4
2. 소스코드
1회차
- 전형적인 구현문제. 함정도 없고, 매우 정직한 문제. 그냥 의식의 흐름대로, 직관적으로 풀었다.
- 예상 시간 복잡도
1) 입력 : N<=20 g<= 10
2 - 1) 한 커브 연산 : O(2^g) [ g <=10 ]
2 - 2) 한 커브 그리기 : O(2^g)
3) 정사각형 찾기 : O(100^2)
총 예상 시간 복잡도 : (2-1) + (2-2) + (3) = O(2^g)
#pragma warning (disable : 4996)
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
using namespace std;
const int pSize = 101;
bool map[pSize][pSize];
int numCv, answer;
int dx[] = { 0,-1,0,1 };
int dy[] = { 1,0,-1,0 };
void drawDC(int x, int y, int dir, int gen) {
// 해당커브의 세대만큼 반복
vector<int> eachCurve;
eachCurve.push_back(dir); // 0세대 세팅
for (int i = 0; i < gen; ++i) { // 1세대부터 반복시작
stack <int> temp;
for (int j = 0; j < eachCurve.size(); ++j) {// stack에 옮기고
//방향바꿔서 스택에 삽입
temp.push((eachCurve[j] + 1) % 4); // 방향// 오 0 위 1 왼 2 아 3
}
while (!temp.empty())//stack에 빌때까지
{
eachCurve.push_back(temp.top());
temp.pop();
}
}
//한 세대 방향을 따라 그린다.
map[x][y] = 1; // 첫점찍고.
for (int i = 0; i < eachCurve.size(); ++i) {
x += dx[eachCurve[i]];
y += dy[eachCurve[i]];
map[x][y] = 1;
}
// 다그림!
}
void findDC() {
for (int i = 0; i < pSize - 1; ++i) {
for (int j = 0; j < pSize - 1; ++j) {
if (map[i][j] && map[i + 1][j] && map[i][j + 1] && map[i + 1][j + 1] )
answer++;
}
}
cout << answer << '\n';
}
int main() {
cin >> numCv;
for (int i = 0; i < numCv; i++) {
int x, y, dir, gen;
cin >> y >> x >> dir >> gen;
drawDC(x, y, dir, gen);
}
findDC();
return 0;
}'알고리즘 > BOJ(백준)' 카테고리의 다른 글
| [백준-17345165번 / 완전탐색 ] 배열 돌리기 4 (삼성SW) (0) | 2020.04.19 |
|---|---|
| [ 백준-17825번 / 완전 탐색 ] 주사위 윷놀이 (삼성기출) (0) | 2020.04.16 |
| [ 백준 - 17822번 / 시뮬레이션 ] 원판 돌리기 (삼성 SW) (0) | 2020.04.14 |
| [ 프로그래머스-lv2 / 진법변환 ] 124 나라의 숫자 (0) | 2020.04.10 |
| [ 프로그래머스-lv2 / 완전탐색 ] 소수 찾기 (0) | 2020.04.09 |

